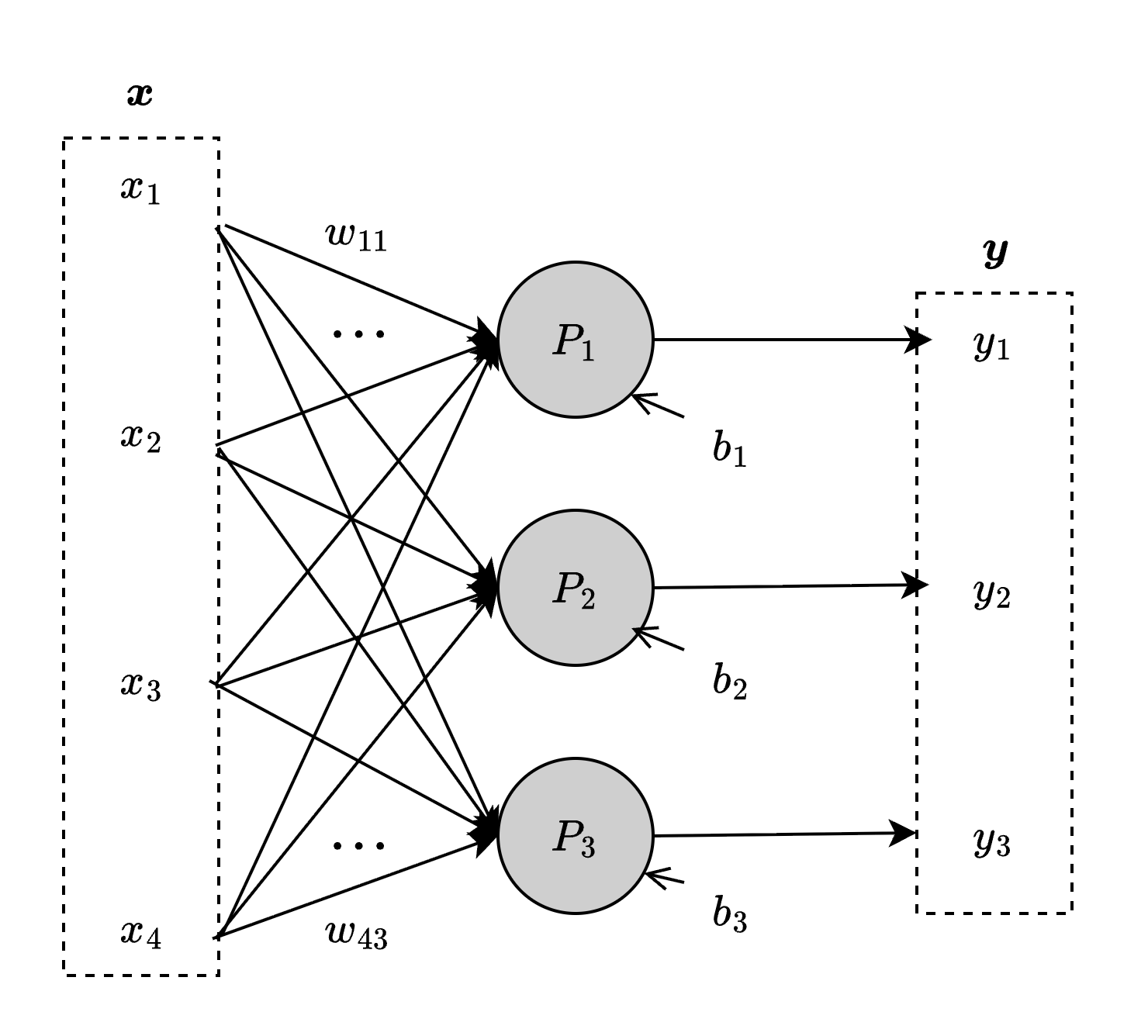
1. Single-Layer Perceptron
Single-Layer Perceptron (SLP) is one of the simplest neural network architectures. It processes an input vector through a linear combination of weights and an activation function to generate an output.
To produce an output vector, the SLP uses one perceptron for each scalar element in the output.
-
In this image, $P_{1},\ P_{2},\ P_{3}$ are perceptrons that produce an output vector of size 3.
-
There are no interactions between these perceptrons, since they are not connected to each other.
-
Each perceptron generates one element of the output vector $y$ from the input vector $x$ using its own weight vector and bias.
-
For example, the first perceptron $P_{1}$ produces the output $y_{1}$:
- weight vector: $(w_{11},\ w_{21}, \ w_{31}, \ w_{41})$
- bias: $b_{1}$
- inputs: $x_{1}, \ x_{2}, \ x_{3}, \ x_{4}$
- The output of this perceptron can be written as the linear combination of the inputs and weights plus the bias:
$$ y_{1}=x_{1}w_{11} + x_{2}w_{21} +x_{3}w_{31} +x_{4}w_{41} + b_{1} $$
This can be generalized for the entire output vector in matrix form as:
$$ y = Wx + b $$
where $W$ is the weight matrix containing the weights for all perceptrons, $x$ is the input vector, and $b$ is the bias vector.
An activation function (such as the step function, sigmoid, or ReLU) is then applied element-wise to the output vector $y$ to introduce non-linearity and produce the final output of the perceptron layer.
Parameter: The values (weights and biases) that define the behavior of a perceptron and are updated during training.
Layer: A layer is a collection of perceptrons in a neural network.
Output layer: The final layer is called output layer.
Hidden layer: Layers that lie between the input and output layers are called hidden layers, and they process the inputs before passing results to the output layer.
Note that the Single-Layer Perceptron has limitations: it can only solve linearly separable problems and cannot model more complex functions like the XOR problem, which requires non-linear decision boundaries.